Em um problema sem solução exata, como ainda assim obter informações relevantes? (V.5, N.9 P.4, 2022)
Tempo estimado de leitura: 5 minute(s)

Capa: Protoboard. Fonte: [1] sob licença CC BY-SA 3.0 [2].
Em uma postagem anterior neste blog [3], nós discutimos um circuito elétrico com uma fonte e dois resistores em série. Considerando os resistores como a incógnita do problema, há apenas uma equação e duas incógnitas, ou seja, o sistema é subdeterminado e o problema poderia ter infinitas soluções. Agora queremos discutir o circuito com resistores em paralelo da Figura 1.
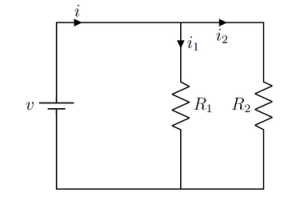
Figura 1: Uma fonte de tensão e dois resistores em paralelo. Fonte: Próprio autor.
Sabendo que a tensão elétrica no resistor R1 é igual à do resistor R2, escrevemos as duas equações que queremos: v = i1R1 e v = i2R2. Para discussão sobre esse tipo de circuito, ver a publicação [4].
Como primeiro caso, vamos considerar os resistores como incógnitas e que é possível medir a tensão e as correntes indicadas. Isso significa que temos duas equações e duas incógnitas e o problema é determinado, isto é, é possível calcular os valores de R1 e de R2. Considerando v = 2 volts, i1 = 0.1 ampères e i2 = 0.5 ampères. Assim, R1 = 20Ω e R2 = 4Ω.
Como segundo caso, vamos considerar a própria tensão como incógnita: Se eu conheço R1 e R2, eu posso medir i1 e i2 e utilizar esses valores para calcular v. Ou seja, há duas equações, mas apenas uma incógnita, um sistema sobredeterminado. Caso não haja nenhum tipo de erro nas medidas, é possível calcular v, mas quando há erros nas medidas, pode ser que resulte em dois valores de v diferentes, tornando o sistema sem solução. Utilizando os mesmos valores do exemplo anterior: i1R1= 0.1×20 = 2 volts e i2R2= 0.5×4 = 2 volts.
E se a gente tivesse um erro nas medidas, mesmo que pequeno? Vamos considerar os seguintes valores: i1= 0.099 ampères, R1= 19.5 Ω, i2 = 0.51 ampères e R2= 4.01Ω. Calculando os novos resultados, obtemos: i1R1= 0.099×19.9 = 1.9701 volts e i2R2= 0.51×4.01 = 2.0451 volts. Os valores são diferentes. Esse é um ponto interessante, pois o modelo do circuito pode até estar correto, mas com medidas do mundo real, sujeitas a erros, nem sempre haverá concordância entre o modelo e elas.
Sob o ponto de vista da álgebra linear o problema se tornou impossível. Qual é o resultado certo? Em outras palavras, qual é a solução aproximada menos errada? Se não podemos obter a solução exata, a solução aproximada pode ser suficiente para fins práticos. Se a gente tiver vários resistores disponíveis é possível, por exemplo, calcular medidas estatísticas como média e desvio padrão para caracterizar a grandeza (tensão) desejada. Outra opção é utilizar algum critério para chegar na resposta final, como o método dos mínimos quadrados para obter informações desse sistema [5, págs. 16-7].
O último caso que queremos comentar é quando adicionamos uma segunda fonte de tensão ao circuito, conforme Figura 2, e consideramos as duas tensões elétricas como incógnitas, v1 e v2. Temos duas equações para tentar resolver o problema?
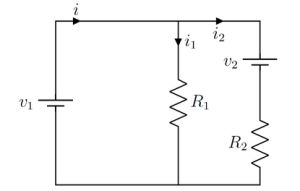
Figura 2: Duas fontes de tensão e dois resistores em paralelo. Fonte: Próprio autor.
Utilizando a lei das malhas, a malha da esquerda resulta em v1 – i1R1 = 0, enquanto a malha da direita obtemos v2 + i2R2 – i1R1 = 0. Se considerarmos que temos acesso às medidas de i1, i2, R1 e R2, o cálculo de v1 e de v2 é possível. Isso significa que, de certa forma, adicionar uma segunda fonte trouxe uma nova incógnita, mas ajudou a tornar o sistema possível e determinado. Conforme [5, págs. 23-4], enquanto o circuito da Figura 1 não é considerado controlável, o circuito da Figura 2 é controlável e podemos começar a fazer relações entre conceitos a princípio abstratos da álgebra linear e conceitos de objetos do mundo físico, como circuitos elétricos.



