Em um problema com infinitas soluções, como escolher a solução certa? (V.5, N.5 P.3, 2022)
Tempo estimado de leitura: 4 minute(s)

Capa: Resistores comerciais. Fonte: [1] sob licença CC BY-SA 3.0.
Na década de 1990, em uma revista vinculada à um software[2], o autor da publicação definiu “o problema impossível mais simples do mundo”. Ele fez a seguinte pergunta: ”Estou pensando em dois números. A média deles é 3. Quais são os números?”. Isso matematicamente pode ser traduzido pela equação 0,5 (x1 + x2) = 3.
A equação acima pode ser simplificada como a soma de duas incógnitas (x1 + x2) resultando em um valor constante (=6), isto é, x1 + x2 = 6. Da álgebra linear, sabemos que esse problema é classificado de subdeterminado e apresenta infinitas soluções. Algumas soluções são:
- x1 = 3, x2 = 3 • x1 = 6, x2 = 0 • x1 = 23, x2 = -17,
mas diversas outras seriam possíveis.
Ao invés de continuar com o exemplo da média, a nossa ideia é discutir que problemas desse tipo podem modelar problemas conhecidos, atribuindo significados físicos para as incógnitas. Sejam dois resistores diferentes, R1 e R2, ligados em série no circuito mostrado abaixo na Figura 1. Com a fonte V ligada, a corrente I é a mesma nos dois resistores e a relação entre as variáveis é V = I (R1 + R2).
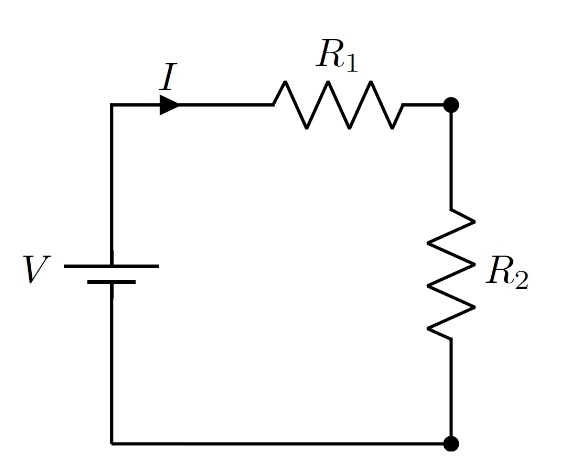
Figura 1: Resistores em série. Fonte: Próprio autor.
Agora vamos imaginar a seguinte situação: O circuito é uma caixa preta da qual não temos acesso direto, conforme Figura 2. As únicas informações que conseguimos medir são a tensão e a corrente, mas o que queremos realmente saber são as resistências de R1 e R2.
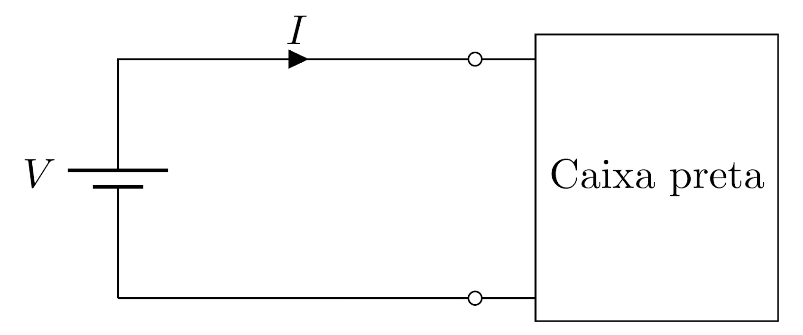
Figura 2: Circuito caixa preta. Fonte: Próprio autor.
Nesse caso, a equação anterior pode ser escrita como V/I = R1 + R2, e que, mais uma vez, resulta em uma constante (lado esquerdo da equação) e duas incógnitas (lado direito da equação). Observamos que se a gente considerar V/I = 3 [V/A], obtemos basicamente a mesma formulação matemática do problema subdeterminado da média, citado anteriormente, mas obtido de um contexto diferente. Nesse caso, como é um sistema físico que está sendo modelado, o fato do problema apresentar infinitas soluções faz com que ele seja chamado de um problema malposto.
De fato, por se tratar de um problema cujos significados físicos são importantes, algumas soluções para R1 e R2, matematicamente possíveis, já podem ser descartadas. Por exemplo:
- Não vamos esperar que esses valores sejam negativos;
- Vamos considerar que há exatamente dois resistores;
- Mesmo considerando que uma das resistências seja muito maior do que a outra, nenhuma das duas será nula;
- Além disso, resistores comerciais têm valores de resistência conhecidos e padronizados, o que também limita os valores possíveis.
Isso significa que quanto mais informações tivermos sobre os resistores, mesmo antes de medir V e I, poderemos restringir as soluções possíveis e direcionar a nossa solução. Esse tipo de conhecimento está disponível antes das medições de informação a priori. Por exemplo, se a gente sabe que os resistores são idênticos, o valor de cada resistência vale 1,5Ω; se a resistência de R1 vale o dobro de R2, R1 = 2 Ω e R2 = 1Ω; e assim por diante.
Talvez não seja possível adivinhar os dois números que uma pessoa esteja pensando (a leitura da mente sim que é impossível), mas quando se trata de um sistema físico, com modelo subdeterminado, podemos fazer algumas hipóteses e achar soluções que, se não forem exatas, pelo menos podem fazer sentido e ter resultados práticos. Esse é o objetivo de uma área de pesquisa que estuda problemas inversos e que desenvolve diversas técnicas para solução deles [3].
Referências
[2] https://blogs.mathworks.com/cleve/2019/07/08/the-worlds-simplest-impossible-problem/
[3] Neto, Antônio, and Francisco D. Neto. Problemas inversos : conceitos fundamentais e aplicações. Rio de Janeiro: EdUERJ, 2005.