Quatérnions: uma descoberta (V.4, N.12, P.4, 2021)

Tempo estimado de leitura: 12 minute(s)

Noções de forma e quantidade são características existentes desde a Pré-história. Para muitos povos antigos e até algumas tribos existentes na Amazônia, ainda que a ideia de quantidade se resuma a diferenciar um, dois e muitos, não há dúvidas de que tais noções estão presentes. Com o desenvolvimento da caça, a formação de rebanhos e o início da agricultura, surge a necessidade de sistematizá-las. E assim surgem os números.

 

Desnecessário dizer que hoje a matemática é muito mais complexa e para seu desenvolvimento o processo de abstração é fundamental. Tal processo, dentre outras vantagens, permite conectar diferentes áreas e proporciona um entendimento profundo de seus problemas. 

 

Dos números naturais, utilizados para uma simples contagem, aos números complexos, há muita história a ser contada. Neste texto, vamos apresentar algumas ideias para introduzirmos nosso assunto principal: os quatérnions. 

 

Matemáticos babilônicos já sabiam resolver equações de segundo grau. Após anos e alguns avanços, estudiosos indianos publicaram a conhecida fórmula de Bhaskara embora ela deva ser atribuída à Sridhara (870-930) que foi quem a escreveu pela primeira vez. Algumas soluções de equações quadráticas envolvem raiz de número negativo, mas até meados do século XVI, os matemáticos descartavam este problema dizendo que se isso ocorresse, tal equação não teria solução. E quando isso mudou?

 

Os números complexos começam a se estabelecer na tentativa de Tartaglia (1499-1557) de resolver uma equação algébrica de grau três. O matemático considerou uma equação cujas raízes reais já eram conhecidas, mas o método sugerido por ele para obtê-las levava à extração da raiz quadrada de números negativos. Neste ponto, os matemáticos não poderiam mais ignorar o problema e assim, os números complexos começam a tomar forma.

 

Em 1777, o matemático suíço Leonhard Euler (1707-1783) introduziu a notação usada hoje, substituindo √-1 por i e começou a estudar os números da forma a + b i, onde a e b são números reais e i é nova unidade imaginária que satisfaz a igualdade i² = -1. Números desta forma são chamados de números complexos. Além disso, eles receberam uma interpretação geométrica: o eixo horizontal (abscissas) representa a parte real a e o eixo vertical (ordenadas) a parte imaginária b. Desta forma, é possível associar a cada ponto do plano ou a cada par ordenado, um número complexo. Assim, a + b i é representado pelo ponto (a, b). Por exemplo, o ponto (1,1) no plano representa o número complexo 1+ i.

 

Em 1833, o matemático irlandês Sir Willian Rowan Hamilton (1805-1865) apresentou um artigo à Academia Irlandesa com os resultados que mostram que pontos no plano, descritos anteriormente, formam um sistema numérico com soma e multiplicação definidas de maneira análoga àquelas feitas para os números complexos. Ou seja, podemos somar e multiplicar pontos no plano. 

 

Uma consequência disso é possibilidade de representar as rotações no plano através de operações algébricas. Por exemplo, pense no ponto (1,0) representado no plano. Agora, suponha que você coloque a ponta seca do compasso na origem (0,0) e a outra ponta sobre o ponto (1,0). Gire o compasso, no sentido anti-horário, de 90°. Em qual ponto você chegou? Essa operação leva a ponta do compasso ao ponto (0,1). Você acabou de fazer uma rotação. Uma característica importante é que a distância do ponto original ou final até a origem se mantém constante, independentemente de quantas vezes, sentido ou ângulo você gire o compasso. 

 

Hamilton permitiu que essa operação fosse feita algebricamente. Para rotacionar um ponto em torno da origem em 90°, basta multiplicar o número complexo que o representa pela unidade imaginária i. No exemplo dado, o número complexo associado ao ponto (1,0) é 1 + 0i. Se multiplico esse número por i, obtenho (1+0i).i= 1i + 0 i² = 1i + 0    Logo, o ponto associado a este número é o (0,1). 

 

Com o objetivo de estender essa ideia para realizar rotações em três dimensões, Hamilton acrescentou uma unidade imaginária aos números complexos. Os chamados tripletos possuíam a seguinte forma: a+bi+cj, onde a, b e c são números reais que definiriam um ponto no espaço tridimensional e i, j são unidades imaginárias tais que i² = j² = -1. Porém, quando multiplicamos os tripletos, surgem termos que apresentam as duas unidades imaginárias multiplicadas, ij e ji, que ainda não haviam sido definidos. Basicamente, queremos que somas e multiplicações de elementos de um determinado conjunto mantenham suas características, ou seja, que continuem sendo elementos desse mesmo conjunto o que não ocorre neste caso já que não conhecemos os elementos ij e ji.

 

Hamilton trabalhou por mais de uma década neste problema. As histórias contadas sobre este episódio sempre citam seu filho que lhe perguntava todas as manhãs: “Papai, você já sabe multiplicar tripletos?” E Hamilton respondia: “Não filho, eu só sei somá-los e subtraí-los”.

 

Para contornar este problema, vamos citar um aspecto importante desse novo conjunto de números. Como já mencionado, rotações mantém uma importante característica que é: a distância do ponto original ou do rotacionado até a origem não se altera. Um simples cálculo, utilizando o teorema de Pitágoras, mostra que a distância é dada pelo valor a² + b² (mais precisamente, é a raiz quadrada desse valor). Algebricamente, esse valor é calculado como (a+bi)(a-bi) =a² – abi + bai + b² = a² + b². Esse resultado é um número real, afinal representa a distância. Note que para os tripletos, temos: (a+bi+cj)(a-bi-cj) = a² + b² + c² + bc(ij + ji) mas, novamente, utilizando Pitágoras sabemos que a distância do ponto (a,b,c) até a origem (0,0,0) é a² + b² + c². Desta forma, para que a analogia funcione temos que impor que ij + ji = 0. Mas isso significa que ij = -ji, o que mostra que a ordem dos fatores altera o produto! Hoje pode parecer simples, mas no final do século XIX essa foi uma ideia revolucionária: abandonar a propriedade comutativa da multiplicação. 

 

Outro problema a ser resolvido era que o produto de dois tripletos deveria ser um tripleto. Tarefa insolúvel. Para resolver isso, uma nova unidade imaginária precisava ser introduzida. À unidade nova foi atribuída a letra k, com a propriedade que k² = -1, e os números que possuem a forma q = a + bi + cj + dk foram nomeados de quatérnions.

 

A ideia de introduzir mais uma unidade imaginária veio ao Hamilton no dia 16 de outubro de 1843, enquanto passeava pela ponte de Brougham, no subúrbio de Dublin. Nesse mesmo lugar, o matemático tirou um canivete do bolso e arranhou em uma pedra a fórmula fundamental de multiplicação dos quatérnions:

 

I² = j²= k² = ijk = -1.

 

 

Imagem 1: Placa em homenagem ao Hamilton na ponte de Brougham, Dublin.

 

Análogo aos números complexos, quatérnions podem ser representados como pontos (a,b,c,d) em 4 dimensões. Em particular, pontos onde a primeira coordenada é nula estão no espaço 3-dimensional e multiplicações destes números por quatérnions de tamanho um estão associadas às rotações no espaço. Desta forma, a não comutatividade fica evidente em um exemplo simples que analisa as rotações de vetores ou pontos no espaço. Rotacionando um vetor com extremidade no ponto A sobre o eixo x em um ângulo de 90° em torno do eixo z, como está mostrado na figura abaixo, é obtido um vetor que se localiza no ponto B sobre o eixo y. Realizando uma rotação, também de 90°, em torno do eixo y, o vetor permanece o mesmo. Se a ordem que realizamos as rotações é invertida, primeiro é obtido o vetor que se localiza na parte negativa do eixo z com extremidade no ponto C e, após a rotação em torno do eixo z, a extremidade permanece no mesmo ponto. Como os pontos B e C são distintos, conclui-se que a rotação no espaço 3-dimensional não é comutativa. Outra maneira simples de pensar na não comutatividade é lembrar que rotações também são feitas através de matrizes e a multiplicação matricial não é comutativa.

 

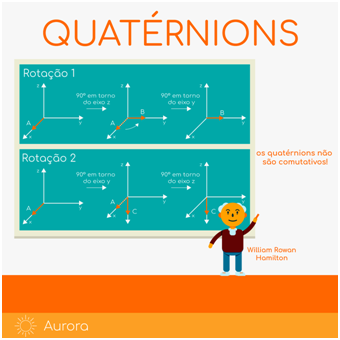
Imagem 2:  Rotações não comutativas no espaço 3D – Aurora UFABC

 

Hoje os quatérnions são uma ferramenta útil em Programação. Para rotacionar algum objeto em três dimensões, na maioria das vezes, é mais prático realizar a multiplicação por um quatérnion do que por uma matriz 3×3. Isso se deve ao fato de que o quatérnion é representado por, no máximo, quatro termos, e, por isso, ocupa menos memória do que a matriz que contém nove.

 

A divulgação da teoria dos quatérnions se deu principalmente à obra do físico James Clerk Maxwell (1831-1879) que usou os métodos desenvolvidos por Hamilton no seu livro “Um Tratado sobre Eletricidade e Magnetismo” publicado em 1873. Infelizmente, a nova álgebra foi rejeitada por muitos matemáticos da época. Em 1884 foi publicada a segunda edição do “Tratado” que continha uma notação mais simples de equações baseadas em cálculo vetorial recém-apresentados. Porém vale ressaltar que os conceitos de produtos escalar e vetorial ensinados hoje foram inspirados a partir da pesquisa do Hamilton.

 

Rotações tridimensionais estão estreitamente relacionadas ao movimento rotacional de um corpo rígido o que faz dos quatérnions uma ferramenta interessante em áreas como astronáutica, robótica, animação digital ou biomecânica do movimento humano. Além de proporcionar uma forma elegante de descrever tais rotações, evita o chamado “gimbal lock”. Este problema consiste na perda de um grau de liberdade na rotação de um objeto em 3 dimensões. Isso ocorre devido ao alinhamento de um dos eixos de rotação com o outro. A nave espacial Apollo 11, que realizou o primeiro pouso na lua, sofreu um incidente com gimbal lock. A equipe estava ciente de que o problema poderia ocorrer, mas ao invés de adicionar mais um eixo de rotação, preferiu usar um indicador que seria acionado perto da situação de perda de um dos graus de liberdade. Quando isso aconteceu, a nave foi movida manualmente usando as estrelas como referência.

 

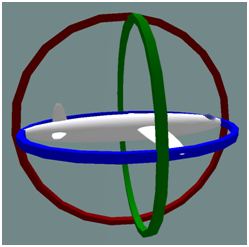
Imagem 3: Dois dos três eixos de rotação estão no mesmo plano, um grau de liberdade é perdido – Wikipedia

 

Além dessas aplicações mais práticas, os quatérnions também proporcionam investigações em Física, em especial, em Mecânica Quântica. Um exemplo é o estudo de equação de Schrödinger, que descreve como uma função de onda evolui no tempo em presença de um potencial descrito por um quatérnion, ao invés de um potencial real. A resolução da equação neste contexto traz as soluções mais gerais do que as já estabelecidas pela Mecânica Quântica usual e, em alguns casos, diferenças qualitativas.

 

Sabemos que os números reais não são suficientes para descrever uma função de onda em Mecânica Quântica, os complexos fazem isso muito bem, porém a necessidade de descrição por uma álgebra quaterniônica não está descartada. Estudos experimentais podem ajudar a definir qual das estruturas algébricas descreve melhor a realidade. Vale dizer que há outros números hipercomplexos utilizados para este fim, mas os quatérnions constituem a álgebra de maior dimensão onde toda divisão é possível (exceto divisão por zero) e vale a propriedade associativa da multiplicação.

 

Referências Bibliográficas:

1. EVES, Howard Whitley. Introdução à história da matemática. Unicamp, 1995.
2. HAMILTON, William Rowan. Elements of quaternions. London: Longmans, Green, & Company, 1866.
3. Cerri, C e Monteiro, M S (2001). História dos Números Complexos. Centro de Aperfeiçoamento de Ensino de Matemática, IME, USP disponível em  https://www.ime.usp.br/~martha/caem/complexos.pdf.
4. PenguinMaths. (2020, Julho 30). How quaternions produce 3D rotation | Animated Math. [Video File]. Disponível em https://www.youtube.com/watch?v=jTgdKoQv738.
5. Adler, S. L. (1995). Quaternionic quantum mechanics and quantum fields, International series of monographs on physics (Oxford, England), 88, Oxford University.
6. ADLER, Stephen L. Peres experiment using photons: No test for hypercomplex (quaternionic) quantum theories. Physical Review A, v. 95, n. 6, p. 060101, 2017.