Buracos de minhoca, o que são? (V.8, N.6, P.4, 2025)

Tempo estimado de leitura: 11 minute(s)

Hoje em dia, “buraco negro” e “buraco de minhoca” são expressões comuns em noticiários, filmes e livros. Buracos negros foram preditos por Schwarzschild em 1916, e por muitos anos eles foram objetos hipotéticos de apenas interesse dos fisícos teóricos, no entanto, recentemente, eles foram observados no centro de galá xias e agora fazem parte da realidade. Nós gostaríamos de falar sobre os buracos de minhoca, que ainda são objetos hipotéticos.

Ch. Misner e J. A. Wheeler

Os primeiros físicos a considerarem buracos de minhoca atravessáveis foram Charles W. Misner e John A. Wheeler em 1957 [1]. Eles propuseram pensar em cargas e massas como buracos no espaço – “cargas sem carga” e “massas sem massa”. Eles alegaram que tudo é uma topologia não tri vial (espaço com buracos) do espaço. Por exemplo, um observador ve um elétron mas acha um buraco invés de uma partícula. Uma partícula com carga negativa (elétron) é conectado com uma partícula de carga positiva (pósitron) e o tubo que os conecta, eles propuseram chamar “buraco de minhoca”. Wheeler é também o autor das palavras “buraco negro” e “buracos negros peludos”.

Vamos primeiro considerar a gravidade na estrutura de Einstein. As estrelas, planetas, buracos de minhoca e buracos negros nos atraem assim como a Terra faz e o valor de suas forças gravitacionais depende de suas massas e da distância até eles. Distante desses objetos nós não conseguimos distingui-los – mas todos eles nos atraem. A diferença é a geometria do espaço que os cercam.

A teoria geral da relatividade de Einstein é baseada no postulado onde a força gravitacional surge da geometria não euclidiana do espaço em torno de uma massa. Nós podemos imaginar o equivalente de geometria e gravidade da seguinte maneira: colocamos uma massa representando o Sol em um plano revestido de borracha. Sem a massa, o plano possui uma geometria euclidiana – todos os teoremas da geometria escolar são satisfeitos, como o teorema de Pitágras. A massa será atraida pela Terra e o formato do plano será deformado, assim como mostra na Fig. 1.

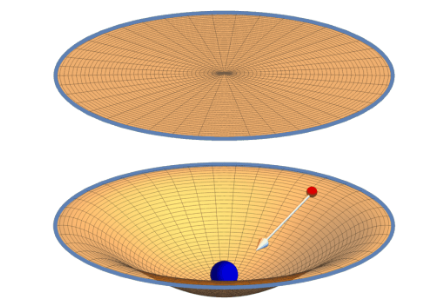
Figura 1: Colocamos uma massa (azul) no disco central do pano revestido de borracha. A geometria curvada representa a gravidade para outra massa (vermelho).

Você pode notar que o teorema de Pitágoras não é mais válido agora – a soma dos ângulos internos não é igual a 180◦. Outra pequena massa é adicionada à grande massa, e isso se parece com a força gravitacional. Então a deformação do espaço nos traz a gravidade e essa é apenas uma anologia para ilustrar o ponto principal de Einstein.

Para ilustrar que o teorema de Pitágoras não é valido para superfícies curvas, vamos considerar a uma simples superfície curva – a esfera, como mostrada na Fig. 2.

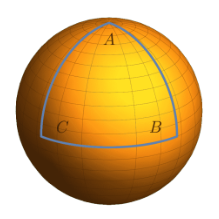
Figura 2: A soma dos ângulos internos do trângulo ABC é igual à 270◦.

Considerando o triângulo ABC, onde AC é o meridiano 0 (Greenwich), AB é o meridiano de 90◦ para o leste, e BC faz parte do equador. Os ângulos do triângulo são ̸ A = ̸ B = ̸C = 90◦. A soma desses ângulos é 270◦ > 180◦. Além disso, existe uma figura da esfera que podemos chamar de “dois-ângulos”, uma analogia ao triângulo, o que é impossível em um espaço euclidiano. Um “dois-ângulos” é uma figura com apenas dois vértices, que pode ser feita, por exemplo, com dois meridianos inteiros do polo norte ao polo sul.

Todo objeto esférico possui um certo raio. As estrelas e os planetas são caracterizados pelos seus próprios. Por exemplo, a Terra tem um raio de R♁ ≈ 6.371 km e o Sol de R⊙ ≈ 696.340 km. Um buraco negro, por sua vez, é caracterizado por um raio específico chamado raio de Schwarzschild RS. Para um buraco negro com a massa da Terra, o raio é RS = 0.88 cm, e para um com a massa do Sol é RS = 2.95 km. Buracos de minhoca também possuem raios específicos, chamados de raio da garganta RT de um buraco de minhoca.

Para ilustrar certas propriedades do espaço de um buraco de minhoca, vamos realizar um simples experimento. Considere um buraco de minhoca com um raio de RG = 2m. Nós ficamos a 1m da garganta do buraco de minhoca (2 + 1 = 3 m do centro da garganta da esfera) e rodeamos o buraco de minhoca com um balão de raio 3m. Para esse balão precisamos de 4π3 ² = 36πm² de material (veja a primeira figura em Fig. 3). Então nos aproximamos 1m do buraco de minhoca e o rodeamos com uma esfera de raio 2m e precisamos de 4π2 ² = 16πm2 de material (veja a segunda figura em Fig. 3).

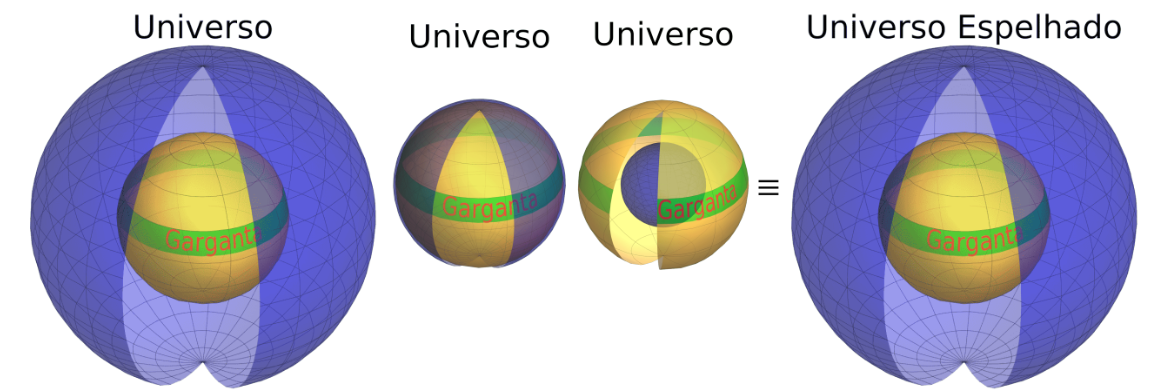
Figura 3: A garganta do buraco de minhoca é representado pela esfera dourada, que é imaginária, na realidade não existe nada lá, e rodeamos a garganta com o balão (esfera azul). Quando vamos através da garganta estamos situados no Universo Espelhado.

Então nós nos aproximamos mais 1m até o buraco de minhoca (veja a terceira figura em Fig. 3). O buraco de minhoca não tem superfície como estrelas ou planetas, o raio RG = 2m é sua característica. Nós realmente entramos no buraco de minhoca e o rodeamos de novo com um balão e descobrimos queprecisamos de 4π3² = 36πm² de material ao invés de 4π1² = 4πm²!

Da perspectiva comum, nós estamos chegando perto do centro da sua garganta, mas nós precisamos de mais material para a esfera com raio 3m. Parece que estamos ficando em 3m de novo. Na realidade, ainda estamos em 3m mas no Universo Espelhado, que é simétrico ao nosso (veja a última figura em Fig. 3). Portanto, nós observamos que, nesse caso, o raio mínimo da esfera que rodeia o buraco de minhoca é igual ao raio de sua garganta. Não há esfera ao redor da garganta que seja menor que a garganta. As esferas com tamanhos menores (até o raio zero) existem, mas estão do lado de fora do buraco de minhoca. Uma esfera que não envolve a garganta de um buraco de minhoca pode ser arrastada para um ponto.

Existe outra observação interessante. Quando vamos dentro do buraco de minhoca em nosso Universo, saímos no Universo Espelhado. Na Fig. 4 a direção do movimento é sinalizada por uma flecha. Em nosso Universo, nós vemos a garganta como uma esfera, mas no Universo Espelhado, nós vemos a esfera pelo lado de dentro. Parece que estamos colocando uma bola de futebol no avesso. Se vamos iluminar por todos os lados o buraco de minhoca em nosso Universo, a sua garganta no Universo Espelhado irá brilhar como uma lâmpada. Portanto, o buraco de minhoca (se existir) deve ser um objeto muito brilhante em ambos universos.

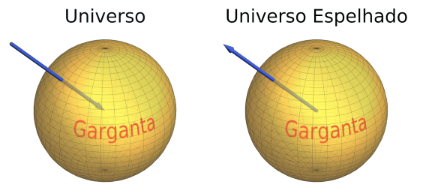
Figura 4: Entramos dentro do buraco de mi nhoca em nosso Universo, mas saímos no Universo Espelhado.

Nós podemos considerar um buraco de minhoca completamente inserido em nosso Universo sem nenhum Universo Espelhado como sugeriu Wheeler. Para fazer esse buraco de minhoca temos que cortar duas esferas no espaço e fazer uma ponte  conectando os limites desses cortes (duas esferas). A primeira esfera (garganta) está situada em um lugar do Universo, mas a segunda, está situada em outra parte do Universo. O tubo que as ligam é chamado de ponte ou alça. O comprimento e formato desse ponte pode ser arbitrário. Nós podemos identificar a segunda esfera com a primeira, que nesse caso possui comprimento zero. Usando essa alça podemos ir dentro da garganta aqui mas sair em outro lugar no mesmo Universo.

Nos livros de ficção científica esse processo é chamado transporte nulo ou T-nulo. Na Fig. 5, que foi pega do artigo [2], o panorama do movimento pelo buraco de minhoca é mostrado. O observador é situado longe do Sistema Solar e consegue ver Saturno pela garganta do buraco de minhoca. Então ele passa pelo buraco de minhoca e imediatamente aparece em Saturno no Sistema Solar.

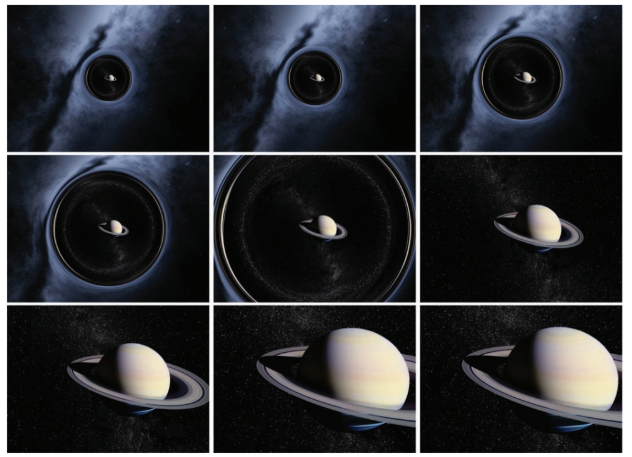
Figura 5: O panorama de viajar pelo buraco de minhoca de outra galáxia diretamente para Saturno [2].

É impossível desenhar essa ponte como uma ponte entre esferas em nosso espaço tridimensional, pois precisamos desenhar  uma alça tridimensional. Para representa-lo, consideramos um universo bidimensional e nesse caso, trocamos as esferas por círculos ou, matematicamente falando, mudamos uma esfera bidimensional S² para uma esfera unidimensional S¹ , que é um círculo. Então nós fazemos o seguinte (veja Fig. 6). O universo é agora um plano bidimensional. Nós cortamos dois discos em lugares diferentesdo universo e faze mos um tubo entre esses circulos, que pode ser chamado de pontes ou alça os conectando. Entre os pontos A e B no universo existem agora dois caminhos AMB e AN B. O último é dentro do tubo ou pelo buraco de minhoca. O comprimento dessa ponte pode ser arbitrário, especialmente muito pequeno. Nesse caso, viajar pelo buraco de minhoca será instantâneo, mesmo se o caminho AMB leve anos-luz.

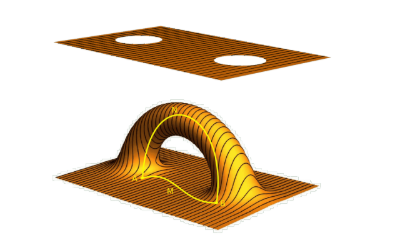
Figura 6: Universo bidimensional. Nós cortamos dois
discos e os conectamos com uma ponte ou alça. Um caminho adicional AN B surge pela alça.

Nós podemos imaginar o caso onde uma ponte menor é mostrada em Fig. 7. O caminho AMB da Terra à uma distante estrela é muito longo, no entanto, o caminho pelo buraco de minhoca AN B pode ser bem rápido e curto. Portanto, os buracos de minhoca são objetos muito prospectivos para viajar por grandes distâncias do universo.

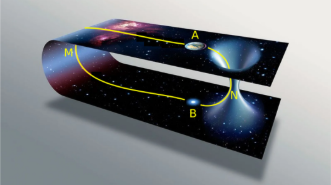
Figura 7: O buraco de minhoca com comprimento pequeno. A distância AN B pelo buraco de minhoca é menor que o caminho usual AMB.

Aqui retornamos ao início para explicar a primeira ideia em que aparecem buracos de minhoca – “cargas sem carga”. Em uma perspectiva física padrão da eletricidade, há um campo elétrico entre uma carga positiva e uma carga negativa, que fornece a atração elétrica entre as partículas carregadas (veja Fig. 8). Misner e Wheeler sugeriu remover partículas, fazendo buracos no espaço e conectá-los com uma alça – um buraco de minhoca. Portanto, não há cargas, mas há um buraco de minhoca e um  campo elétrico. Um observador verá a mesma imagem – duas cargas atrativas. A ideia era muito incomum e atraente, mas agora não é geralmente aceita. A ideia estava equivocada, mas o conceito dos buracos de minhoca permaneceu.

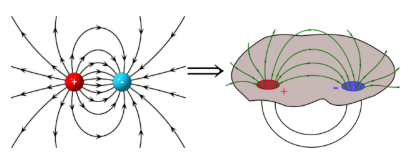
Figura 8: Na figura de Misner e Wheeler duas cargas interativas são consideradas buracos de minhoca.

O principal problema da física do buraco de minhoca é como criar esses objetos ou como encontrá-los no universo. Para criar um buraco de minhoca, nós precisamos de uma matéria extremamente incomum que não existe em nosso universo, os físicos a chamam de “matéria exótica”. Outra possibilidade é desenvolver uma teoria alternativa da gravidade, onde buracos de minhoca possam existir sem matéria exótica, por exemplo, levando em conta a possível existência de dimensões extras. O problema de criar e/ou observar buracos de minhoca ainda está em aberto.

REFERÊNCIAS

[1] C. W. Misner and J. A. Wheeler, Ann. Phys. (N. Y). 2, 525 (1957).

[2] O. James, E. von Tunzelmann, P. Franklin, and K. S. Thorne 10.48550/arxiv.1502.03809 (2015).