Modelando sistemas físicos com matrizes e vetores. (V.5, N.10 P.4, 2022)
Tempo estimado de leitura: 5 minute(s)
Divulgadores: Roberto Gutierrez Beraldo e Ricardo Suyama
Emails: roberto.gutierrez@aluno.ufabc.edu.br e ricardo.suyama@ufabc.edu.br
Capa: Linhas e colunas de uma matriz. Fonte: [1] sob licença CC BY-SA 4.0 [2].
Na matemática do ensino básico, aprendemos a resolver sistemas de equações lineares do tipo
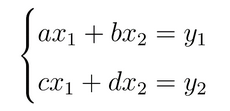
onde a, b, c, d são coeficientes, x1 e x2 são incógnitas e y1 e y2 são termos que não acompanham as incógnitas. Nós também aprendemos operações com matrizes [3], de modo que podemos escrever essas mesmas equações como [4]
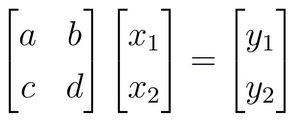
A forma matricial acima pode ser resumida com a notação
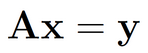
onde A é a matriz de coeficientes, x é o vetor de incógnitas (ou parâmetros do sistema) e y é o vetor dos termos isolados (dados que temos disponíveis) [5]. Diversos problemas podem ser escritos na forma Ax = y [6], incluindo exames de imagens médicas como tomografia computadorizada e ressonância magnética. Para cada uma delas, A, x e y têm significados diferentes, sendo necessário conhecer o problema para formá-los.
Isso também é possível para os circuitos elétricos [7], como apresentados em posts anteriores deste blog “Em um problema com infinitas soluções, como escolher a solução certa?” e “Em um problema sem solução exata, como ainda assim obter informações relevantes?”, que podem ser encontrados pela própria ferramenta de busca do blog.
Figura 1: Uma fonte de tensão e dois resistores em série. Fonte: Próprio autor.
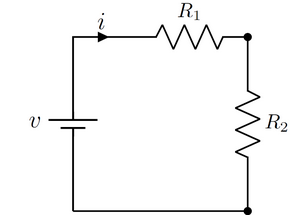
Vamos considerar o circuito da Figura 1, de resistores em série:
A equação que modela o problema é dada por
É possível escrevê-la considerando que a incógnita do sistema é a corrente i:
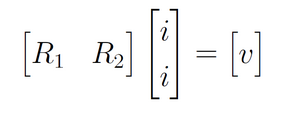
Para deixar na forma de multiplicação de matriz-vetor, podemos adicionar uma equação (linha) redundante (na qual 0=0), conforme
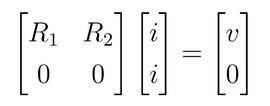
Apesar de ter uma linha nula, é possível resolver o problema quando a corrente é a incógnita e todos os outros dados estão disponíveis. De fato, para montar o problema, sempre vai depender de quais informações temos disponíveis. Se temos disponíveis a corrente e a tensão da fonte, considerando as resistências como incógnitas, a equação se torna
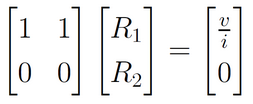
na qual há duas incógnitas, mas apenas uma equação, o que representa infinitas soluções possíveis, conforme discutido em post anterior.
Vamos considerar agora o circuito da Figura 2, de resistores em paralelo:
Figura 2: Uma fonte de tensão e dois resistores em paralelo. Fonte: Próprio autor.
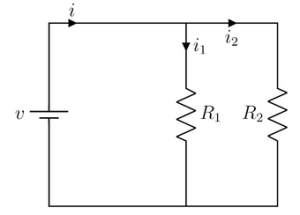
O sistema resultante é dado por
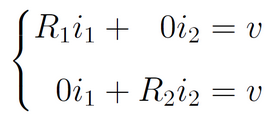
É possível escrever esse sistema considerando, respectivamente, as correntes, as resistências e a tensão como incógnitas, já na forma de matriz-vetor:
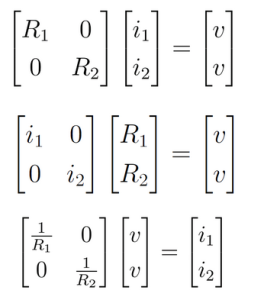
No último caso, quando a tensão v é a única incógnita, há duas equações, um sistema sobredeterminado. Caso as medidas das resistências e das correntes apresentem erros, o sistema pode se tornar impossível de ser resolvido.
Por fim, vamos considerar agora o circuito da Figura 3, com dois resistores em paralelo, mas duas fontes de tensão:
Figura 3: Duas fontes de tensão e dois resistores em paralelo. Fonte: Próprio autor.
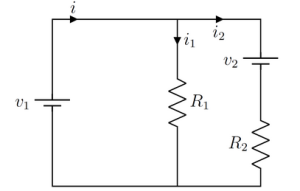
O sistema resultante é dado por
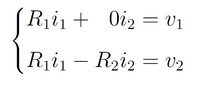
Para considerar as tensões como incógnitas, podemos começar reescrevendo esse sistema como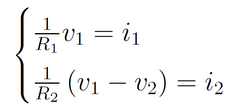
Da qual se obtém-se a forma matricial com duas equações e duas incógnitas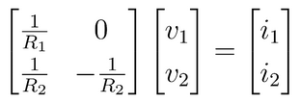
A partir da adição da segunda fonte, o problema deixa de ser sobredeterminado e passa a ser determinado. A notação matricial nem sempre é necessária para a solução de circuitos elétricos, mas pode ser uma forma de se organizar, principalmente em circuitos com muitos elementos.
Referências bibliográficas:
[1] https://commons.wikimedia.org/wiki/File:Matris.png
[2] https://creativecommons.org/licenses/by-sa/4.0/
[3] https://portaldaobmep.impa.br/index.php/modulo/ver?modulo=75
[6] http://www.ime.unicamp.br/~apmat/sistemas-lineares-algumas-aplicacoes/
[7] https://www.ufrgs.br/eng04030/Aulas/teoria/cap_05/metmal.htm
