A tabela verdade da implicação: por que a noite é escura? (V.4, N.8, P.2, 2021)

Tempo estimado de leitura: 9 minute(s)

Divulgador da Ciência:

 

A “Noite Estrelada” de Vincent van Gogh, 1889. https://pt.wikipedia.org/wiki/A_Noite_Estrelada#/media/Ficheiro:Van_Gogh_-_Starry_Night_-_Google_Art_Project.jpg

Uma das pinturas mais famosas do mundo, a Noite Estrelada, foi criada por Vincent van Gogh em 1889. O pintor estava isolado no asilo psiquiátrico de Saint-Paul-de-Mausole, no qual havia se internado em maio daquele ano após ter arrancado sua orelha esquerda ^[1]. O quadro é considerado a mais importante e conhecida obra do pintor holandês ^[2], e atualmente, pode ser apreciada presencialmente pelos poucos privilegiados que têm condições de visitar o Museu de Arte Moderna de Nova York.

 

Em uma carta enviada a seu irmão, van Gogh nos indica de onde veio a inspiração. Ele conta que passou horas olhando a noite de sua janela ^[2] e descreve como ficou impressionado pelo brilho e movimento de Vênus, da Lua e das estrelas. A pintura em óleo sobre tela reflete a visão do seu criador: as estrelas não são pontos, a Lua não é um círculo branco e o movimento dos corpos celestes está expresso no traçado dos pincéis, que contrasta com a noite escura.

 

Curiosamente, se aplicarmos alguns detalhes e uma lógica simples nos leva a concluir que as noites não deveriam ser escuras.

 

Esta proposição é conhecida como o “paradoxo de Olbers”, e é bem fácil de enunciar: dado que o universo é infinitamente antigo, estático e infinitamente extenso e tem um infinito número de estrelas, para qualquer ponto que olharmos no céu haverá uma estrela. Portanto, a noite não deveria ser escura ^[3].

 

O astrônomo e físico alemão Heinrich W. M. Olbers ficou mais famoso por transcrever este paradoxo do que por outras importantes descobertas que fez (por exemplo, ele é o descobridor do asteroide Pallas, em 1802 ^[4]). De fato, vários outros cientistas se debruçaram sobre este problema, dos quais podemos citar Cosmas Indicopleustes (ano ~300), Thomas Digges (em 1556), Johanes Kepler (1610) e Lord Kelvin (1901) ^[5]. Até mesmo o poeta Edgar Allan Poe, em seu ensaio “Eureka” (1848) tratou do assunto ^[6], o que nos leva a concluir que este paradoxo também é um assunto interdisciplinar.

 

Evidentemente, todas essas considerações sobre a noite ser escura ou não levam em conta somente o que conseguimos captar através da nossa visão. Existe instrumentação e tecnologia que, se usada adequadamente, nos mostraria uma noite clara. Contudo, nesta nossa discussão, estamos tratando daquilo que vemos com os nossos olhos apenas.

 

Fique tranquilo, caro leitor, pois, apesar de tantos filósofos por tanto tempo tentarem explicar o paradoxo, posso categoricamente afirmar que a noite continua escura. Para esclarecer o assunto, farei uso de uma ferramenta matemática de fundamental importância: a implicação.

 

Em particular, usaremos a implicação material sob uma perspectiva semântica. A forma mais trivial deste operador funcional sempre nos retorna com a “verdade”, exceto apenas no caso em que o primeiro argumento seja verdadeiro e o segundo argumento seja falso. Sua tabela verdade é a seguinte:

 

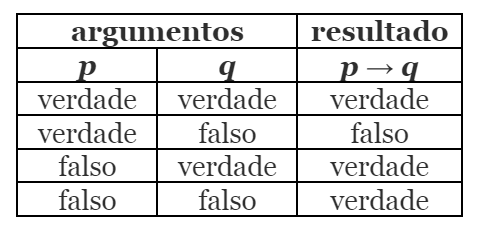
Nesta tabela, p e q são afirmações, e lemos a coluna de resultados, p → q, como “se p então q”. Tomemos um exemplo: “se eu estou na rua quando está chovendo, então estou molhado”. Neste caso, p é “eu estou na rua quando está chovendo” e q é “estou molhado”.

 

Aos meus alunos, sempre que posso, ofereço uma regra mnemônica para esta tabela: somente a verdade não se transforma em falsidade – que corresponde à segunda linha da tabela, a única que resulta em falsidade.

 

Aplicaremos este operador ao paradoxo de Olbers. Imediatamente identificamos o segundo termo: neste caso, q é “a noite não deveria ser escura”. Como a noite é escura, sabemos que q é falso. Portanto, para que a implicação seja verdadeira, adotamos a quarta linha da tabela verdade. Ou seja, temos que provar que o primeiro termo também é falso.

 

O termo p é uma sequência de conjunções, ou seja, afirmações encadeadas pelo operador “e”: o universo é infinitamente antigo “e” estático e infinitamente extenso “e” tem um infinito número de estrelas.

 

Para que o operador “e” resulte em verdade, temos que ter certeza de que todos os seus argumentos sejam verdade. A pergunta que surge é: seria uma destas afirmações falsa?

 

Resposta: sim, todas são falsas.

 

A primeira afirmação, “o universo é infinitamente antigo” é falsa. Atualmente, o Big Bang, a teoria adotada para a origem de tudo o que conhecemos (inclusive o tempo), nos dá como idade do universo cerca de 13,77 bilhões de anos ^[7]. Apesar desse número ser grande, o universo não é infinitamente antigo (mais um conselho prático: se você quiser saber se um número é grande, imagine ser dinheiro).

 

A segunda afirmação: “o universo é estático e infinitamente extenso”, exige uma interpretação mais sutil. Hoje, sabemos que o universo está em expansão. A lei de Hubble-Lemaître ^[8] é resultado direto da observação das galáxias. A partir do deslocamento espectral da luz proveniente das galáxias podemos concluir que estas estão se afastando umas das outras a velocidades proporcionais à sua distância. Ou seja, quanto mais longe elas estão, mais rápido se afastam de nós. 

 

Portanto, o universo está bem longe de ser estático. Como a velocidade de expansão aumenta com a distância, a luz proveniente dos objetos mais longínquos acaba sendo deslocada para o vermelho, sendo este o famoso efeito Doppler [9]. Lembremos que a velocidade das galáxias é determinada pelo desvio da sua luz para o vermelho. Em outras palavras, se recebemos a luz de uma galáxia, conseguimos determinar a velocidade de seu afastamento. Assim, uma estrela localizada “infinitamente” longe terá a sua luz infinitamente desviada para comprimentos de onda invisíveis para nós, seres humanos. Logo, mesmo que o universo “seja infinitamente extenso”, mas não estático, implica que somente veremos as estrelas relativamente próximas de nós.

 

A terceira afirmação, “ter um número infinito de estrelas”, pode até ser verdadeira, mas acaba sendo ineficaz devido ao argumento anterior. Apesar de poder existir infinitas estrelas, como elas estão distribuídas pelo mesmo universo que se expande, não as conseguiremos ver. Além disso, a velocidade da luz é constante (300.000 km/s) e o universo tem uma idade finita. Considerenado as correções devido à expansão do universo, podemos considerar que a luz das estrelas que estão além de 45 bilhões de anos-luz ainda não chegou até a Terra, sendo invisíveis para nós. Uma outra interpretação deste argumento é que não estamos limitados apenas no espaço, mas também, e principalmente, no tempo.

 

Com a evolução do nosso conhecimento sobre a natureza da luz e descobrimentos de outras evidências que se alinham com a teoria do Big Bang, surgiram novos argumentos que também resolvem o paradoxo de Olbers, mas estes outros fatos eu deixarei para outro momento.

 

Assim, a afirmação completa “se o universo é infinitamente antigo, estático e infinitamente extenso e tem um infinito número de estrelas” é falsa.

 

Concluímos reafirmando aquilo que já sabíamos: a noite é escura. E deve continuar assim pelo resto de nossas vidas, para alegria dos boêmios, namorados e pintores. 

 

Caro leitor, da próxima vez que puder, olhe bem para a escuridão da noite. Ela, na sua humilde falta de luz, nos fala muito mais sobre o universo do que o dia mais radiante.

 

Referências

^[1] Naifeh, Steven and Gregory White Smith (2011). Van Gogh: The Life. New York: Random House. ISBN 978-0-375-50748-9.

^[2] Pickvance, Ronald (1984). Van Gogh in Arles. New York: Metropolitan Museum of Art. ISBN 0-87099-376-3.

^[3] D’Inverno, Ray. Introducing Einstein’s Relativity, Oxford, 1992.

^[4] Forbes, Eric G. (1971). “Gauss and the Discovery of Ceres”. Journal for the History of Astronomy. 2 (3): 195–199. Bibcode:1971JHA…..2..195F. doi:10.1177/002182867100200305

^[5] Harrison, Edward R. (1968). “The early universe”. Physics Today. 21 (6): 31–39. doi:10.1063/1.3035005. ISSN 0031-9228.

^[6] Sova, Dawn B. Edgar Allan Poe: A to Z. New York: Checkmark Books, 2001: 82. ISBN 0-8160-4161-X.

^[7] Alpher, Ralph A.; Herman, Robert, “Evolution of the Universe”. Nature. 162 (4124): 774–775. Bibcode:1948Natur.162..774A. doi:10.1038/162774b0. S2CID 4113488.

^[8] IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law” (Press release). International Astronomical Union. 29 October 2018. Retrieved 2018-10-29.

^[9] Doppler, Christian (1846). Beiträge zur fixsternenkunde. 69. Prague: G. Haase Söhne. Bibcode:1846befi.book…..D.