Nonograma, um jogo para aprender o princípio da tomografia (V.6, N.1 P.6, 2023)

Tempo estimado de leitura: 6 minute(s)

Vocês conhecem o jogo chamado nonograma [3]? Ele é jogado em um tabuleiro conforme o apresentado na figura abaixo, composto por uma região quadriculada e um conjunto de números nas margens de cada linha e coluna. O seu objetivo é descobrir qual o padrão escondido de quadrados preenchidos e vazios do tabuleiro. Para isso, devem ser seguidas as indicações dos números presentes nas margens, que trazem informações sobre cada uma das linhas e colunas.

Vamos ver um exemplo (Puzzle ID: 9,809,855 disponível em [4]):

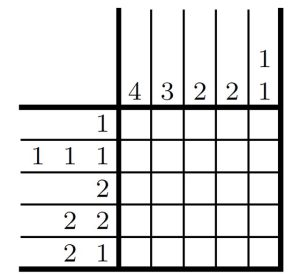
Na terceira coluna, por exemplo, o número 2 indica que existem somente dois quadrados consecutivos preenchidos nesta coluna, com os restantes sendo vazios. No entanto, só essa informação ainda não é o bastante para marcarmos algo no tabuleiro, visto que existem diversas possibilidades que podemos seguir para preencher esses dois quadrados consecutivos dentro dessa coluna.

Por outro lado, se olharmos a segunda linha nós temos os números 1-1-1. Essa sequência indica que nessa linha possuímos 3 quadrados preenchidos de forma que existam um ou mais quadrados vazios entre eles. A única forma possível de atender esse padrão nesse tabuleiro é conforme apresentado na figura abaixo, logo podemos preencher os quadrados.

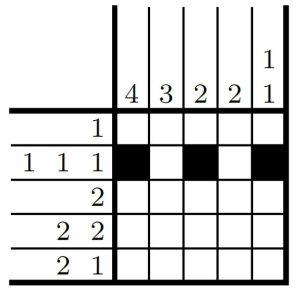
Se olharmos com atenção, podemos ver que a quarta linha também nos dá uma sequência que só pode ser preenchida de uma única maneira: 2-2. Essa sequência indica que existem quatro quadrados preenchidos nessa linha, sendo que existem dois consecutivos, um ou mais vazios e mais dois consecutivos. A única possibilidade de atender a esse padrão é preenchida na figura abaixo.

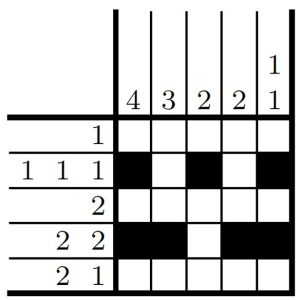
Outro ponto importante desse jogo é que a ordem dos números nas margens importa. Na última linha, por exemplo, a sequência 2-1 indica que temos dois quadrados consecutivos preenchidos, um ou mais vazios e em seguida mais um preenchido. Dessa forma, não seria válido nesse caso ter um quadrado preenchido, um ou mais vazios e em seguida os dois consecutivos preenchidos, já que isso corresponderia à sequência 1-2.

Somente a informação da sequência 2-1 não é o bastante para preenchermos a última linha, visto que teríamos mais de uma possibilidade. No entanto, podemos combinar essa informação com outras que já temos no tabuleiro para resolver esse impasse. Ao olharmos a última coluna, por exemplo, vemos que o padrão 1-1 já é atendido, e os demais quadrados nessa coluna são todos vazios. Dessa forma, só restam os outros quatro quadrados para trabalharmos na última linha, o que faz com que só exista uma forma de seguir o padrão 2-1, apresentada na figura abaixo.

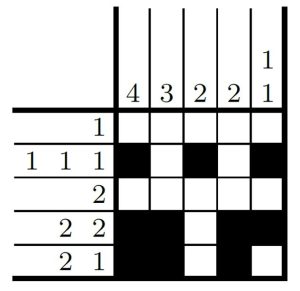
Como podemos ver, à medida que preenchemos o tabuleiro vamos eliminando as possibilidades pelas quais podemos marcar os quadrados atendendo aos padrões indicados em cada linha e coluna. No estado atual, por exemplo, vemos que agora só existe uma única maneira de preencher a primeira coluna atendendo ao padrão de existirem quatro quadrados consecutivos preenchidos, conforme apresentamos a seguir.

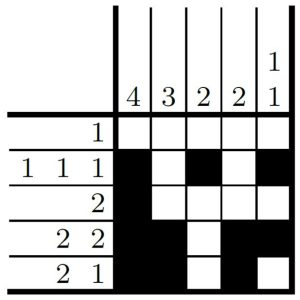
O mesmo se aplica para a segunda coluna, onde precisamos ter três quadrados consecutivos preenchidos, o que fazemos a seguir.

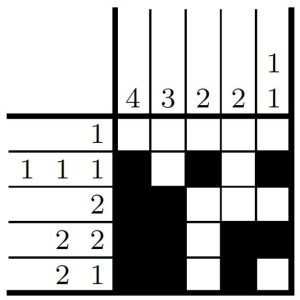
Por fim, ao olharmos a primeira linha, vemos que ainda precisamos preencher um quadrado nela. Se observarmos cada uma das colunas, vemos que a única que ainda não atendeu ao padrão presente na margem é a terceira. Logo, o único quadrado que podemos marcar na primeira linha é o da terceira coluna, como mostramos a seguir.

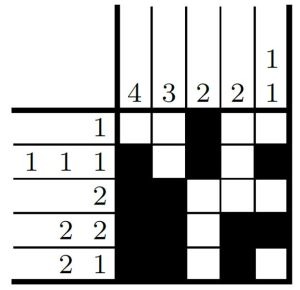
Se checarmos os padrões de cada linha e coluna na figura acima veremos que todos são atendidos corretamente, o que indica que completamos o jogo com sucesso.

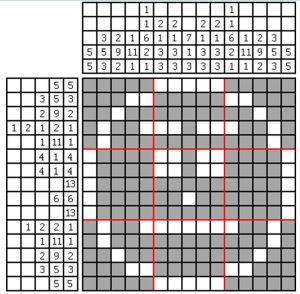
Tanto no site [4] quanto no site [5] há muitos outros desafios, inclusive com tamanhos maiores. Na imagem da capa desta publicação há a letra “W” (inicial de Wikipedia) em 20 linhas por 30 colunas. Na figura abaixo [6],  sob licença CC BY-SA 3.0 [7], há um rosto em 15 linhas por 15 colunas. É claro que com um maior número de linhas e colunas é possível que o desenho represente objetos conhecidos e há alguns realmente complexos, inclusive coloridos, como pode ser visto em [5].

Como o nonograma pode ser visto como mais do que um jogo? O seu princípio pode ser entendido como ter informações externas ao desenho (representado pelas sequências) que devemos usar para reconstruir a imagem de dentro. Essa é a ideia básica da tomografia computadorizada, um tipo de equipamento médico que tem muita importância para diagnóstico de doenças.

Quais são as diferenças? A primeira é que o nonograma é como se fosse uma tomografia discreta [8], no sentido de que cada quadrado só pode ter valores “0 ou 1”, enquanto cada pixel na imagem de tomografia pode ter valores que não sejam binários. Outra diferença é que no nonograma há sequências que são conhecidas. Na imagem do sorriso, por exemplo, há (5,5), (3,5,3), (6,6), (1,2,2,1) etc. Na tomografia computadorizada, as informações externas vêm na forma da soma total: (5,5) seria 10, (3,5,3) seria 11, (6,6) seria 12 e (1,2,2,1) seria 6 . Por fim, no nonograma, há esses valores das sequências para apenas dois ângulos (duas projeções): 0º (horizontal) e 90º (vertical). Na tomografia computadorizada, para compensar esse desconhecimento das sequências, são necessários mais ângulos de projeção. A formação da imagem tomográfica é ilustrada em [9].

Referências bibliográficas:

[1] https://commons.wikimedia.org/wiki/File:Nonogram_wiki.svg

[2] https://creativecommons.org/publicdomain/zero/1.0/

[3] https://en.wikipedia.org/wiki/Nonogram

[4] https://www.puzzle-nonograms.com/

[5] https://www.nonograms.org/

[6] https://commons.wikimedia.org/wiki/File:Paint_by_Number_solution.png

[7] https://creativecommons.org/licenses/by-sa/3.0/

[8] https://en.wikipedia.org/wiki/Discrete_tomography

[9] https://www.youtube.com/watch?v=q7Rt_OY_7tU

* Capa: Nonograma da letra W. Fonte: [1] sob licença CC0 1.0 Universal [2].