O que a altura de um bebê nos ensina sobre overfitting? (V.8, N.6, P.5, 2025)
Tempo estimado de leitura: 9 minute(s)
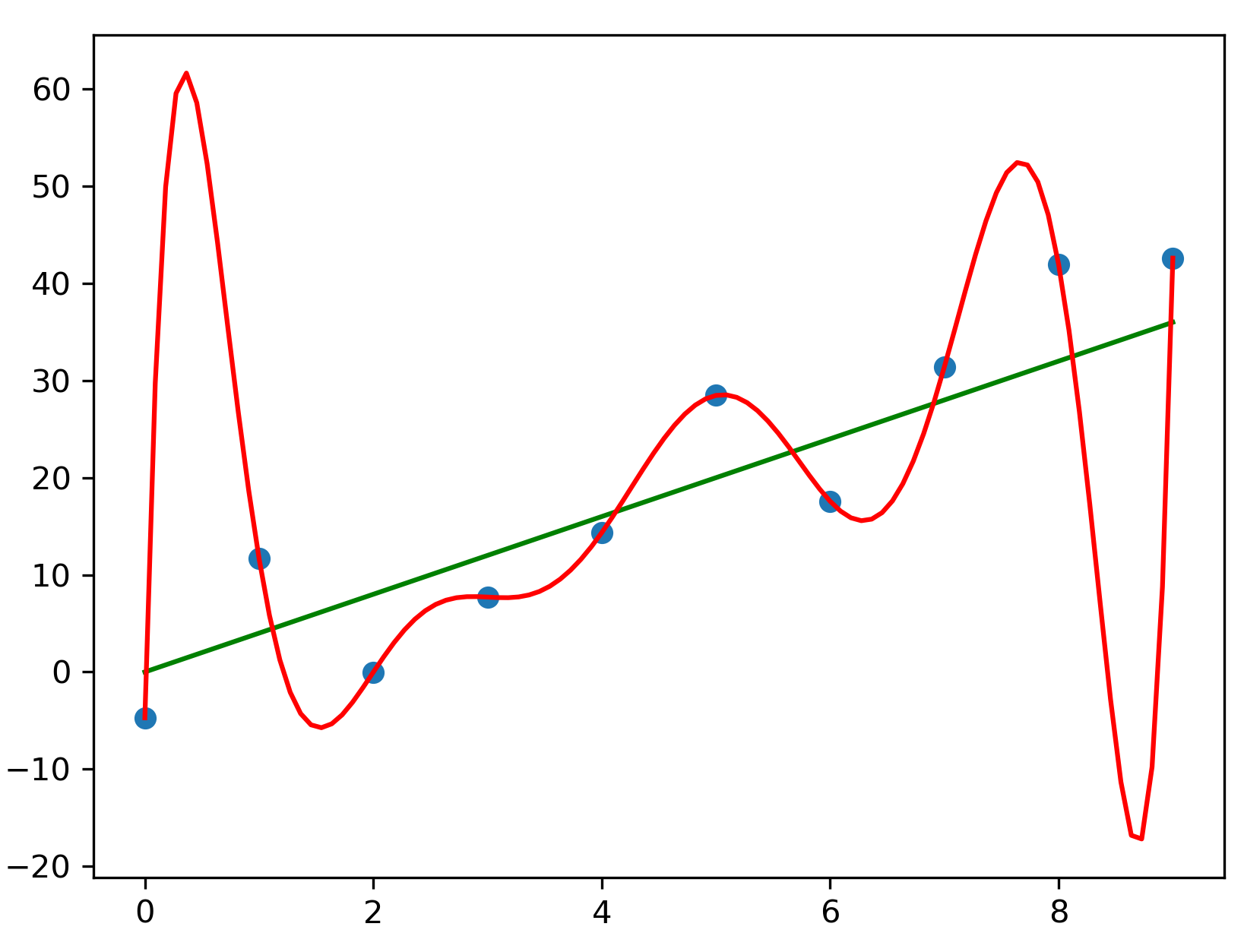
Capa: Exemplo de overfitting nos dados. Fonte: [1], sob licença CC Attribution 4.0 International [2].
Desde que um bebê nasceu, diferentes enfermeiros mediram a sua altura utilizando réguas antropométricas infantis. O resultado é mostrado na Figura 1.
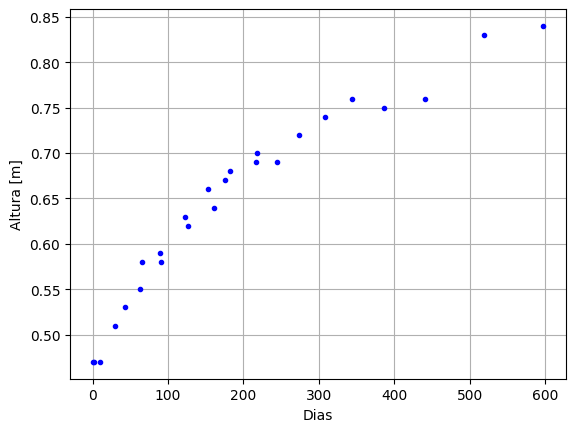
Figura 1: Gráfico de altura de um bebê ao longo de 600 dias. Fonte: Próprio autor.
Em nenhum momento imagina-se que a altura de alguém diminua, mas há pontos no gráfico em que isso acontece. O que é mais provável, que o bebê diminuiu ou que há erros relacionados ao próprio processo de medição? Ir ao médico pode ser estressante para o bebê, ele pode chorar e se mexer no momento de medirem a sua altura, sem garantir que a régua esteja paralela ao eixo vertical do bebê, dificultando as medições. Ao mesmo tempo, pode haver variação na manipulação da régua por diferentes enfermeiros e enfermeiras, o que também causaria variações nos resultados. Em suma, há incertezas experimentais associadas às medidas. Como melhorar a coleta dos dados, para evitar erros sistemáticos e minimizar os erros aleatórios? Obter dados de qualidade diminui a chance dos erros prevalecerem sobre o sinal de interesse. Mesmo com limitações, esses são os dados que estão disponíveis para análise e que devem ser utilizados.
Na sequência, uma questão pode ser feita: Existe algum modelo, relativamente simples, que permita representar os dados de maneira adequada dentro do intervalo original? Considerando que há uma variável dependente (altura) para uma variável independente (data), pode-se realizar uma regressão linear [3]. O resultado é mostrado na Figura 2.
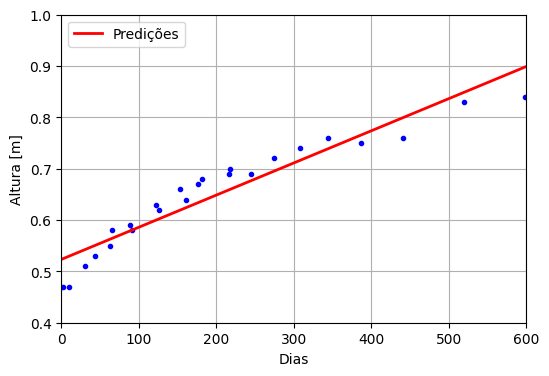
Figura 2: Regressão linear para a altura do bebê ao longo de 600 dias. Fonte: Próprio autor.
Observa-se que os dados iniciam abaixo da reta, passam a ficar acima da reta, e depois voltam a ficar abaixo da reta. Em outras palavras, os dados parecem ter uma tendência inicial de aceleração e depois de desaceleração ao longo dos dias, comportamento que não é capturado pela reta. Pode-se argumentar que a reta não é muito sensível às variações dos dados, situação conhecida como underfitting (ou subajuste), quando o modelo é mais simples do que os dados que se quer representar.
É necessário um modelo que seja capaz de representar dados mais complexos, com mais variação. Um caminho é utilizar a regressão polinomial [3], i.e., em vez de se tentar encontrar uma reta para ajustar os dados, utiliza-se um polinômio de grau definido a priori. Ressalta-se que a própria reta utilizada pode ser considerada um polinômio de grau 1. A Figura 3 mostra o resultado da regressão para um polinômio de grau 2 (parábola).
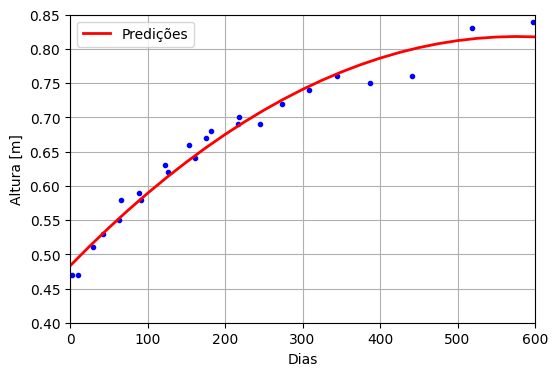
Figura 3: Regressão polinomial de grau 2 para a altura do bebê em 600 dias. Fonte: Próprio autor.
À primeira vista, observa-se que a parábola é capaz de representar a desaceleração ao longo do tempo, mas que os dados a partir de 350 dias começam a ficar distantes da curva. Reconhecendo que a concavidade da parábola está voltada para baixo, o vértice da parábola não deve estar distante, isto é, se ele já não estiver dentro dos 600 dias. Isso justifica a aparente queda de altura nos últimos dias do gráfico.
A Figura 4 mostra o resultado da regressão para um polinômio de grau 8. Observa-se que ele é capaz de representar bastante variação no sinal, tanto que a curva inverte de direção várias vezes, tentando se aproximar dos pontos nas diferentes regiões. É claro que esse comportamento não é adequado e acaba representando o ajuste demasiado nos dados, inclusive naqueles dados que possuem erros mais acentuados. Essa situação é conhecida como overfitting [3], ou sobreajuste aos dados e acontece quando o modelo é capaz de representar dados mais complexos do que o sinal de interesse. O ajuste dele é tão específico que dificilmente esse modelo poderia ser utilizado com dados diferentes.
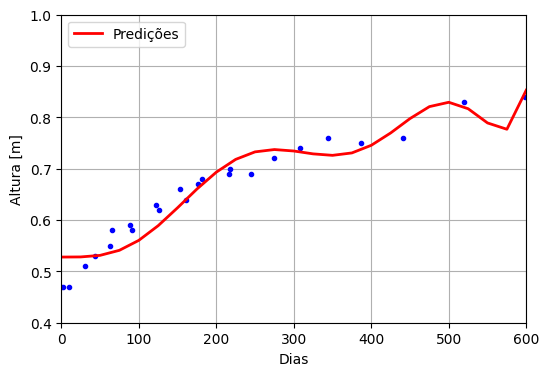
Figura 4: Regressão polinomial de grau 8 para a altura do bebê ao longo de 600 dias. Fonte: Próprio autor.
Apenas com base na observação das curvas é possível dizer qual foi a melhor curva ajustada? Provavelmente não. Um critério objetivo pode ser utilizado, como o coeficiente de determinação [4], que, neste exemplo, é uma forma de medir quanto que o modelo de regressão consegue prever a altura do bebê apenas olhando para o número de dias desde o seu nascimento. Em outras palavras, ele mede se o ajuste da curva foi bom. Quanto mais próximo de 1, melhor.
Tabela 1: Resultados dos ajustes.
| Ajuste: Grau do polinômio | Nota (Coeficiente de determinação) |
| 1 | 0.574 |
| 2 | 0.599 |
| 8 | 0.603 |
É curioso que a parábola seja o pior resultado, já que visualmente ela parece um modelo razoável. No caso do polinômio de grau 8, sua flexibilidade permite que ele tenha uma nota maior, mas ela não é, já que não é uma função monótona estritamente crescente (na fase de crescimento do bebê, ao menos). Ou seja, tem nota maior, mas não é adequada. Às vezes, as métricas enganam.
Outro teste possível é de utilizar o modelo ajustado de 0 a 598 dias em um intervalo maior, até 900 dias por exemplo e mostra se é viável utilizar o modelo em uma situação diferente da que ele foi desenvolvido. A Figura 5 traz os resultados dos modelos anteriores quando utilizados até 900 dias.
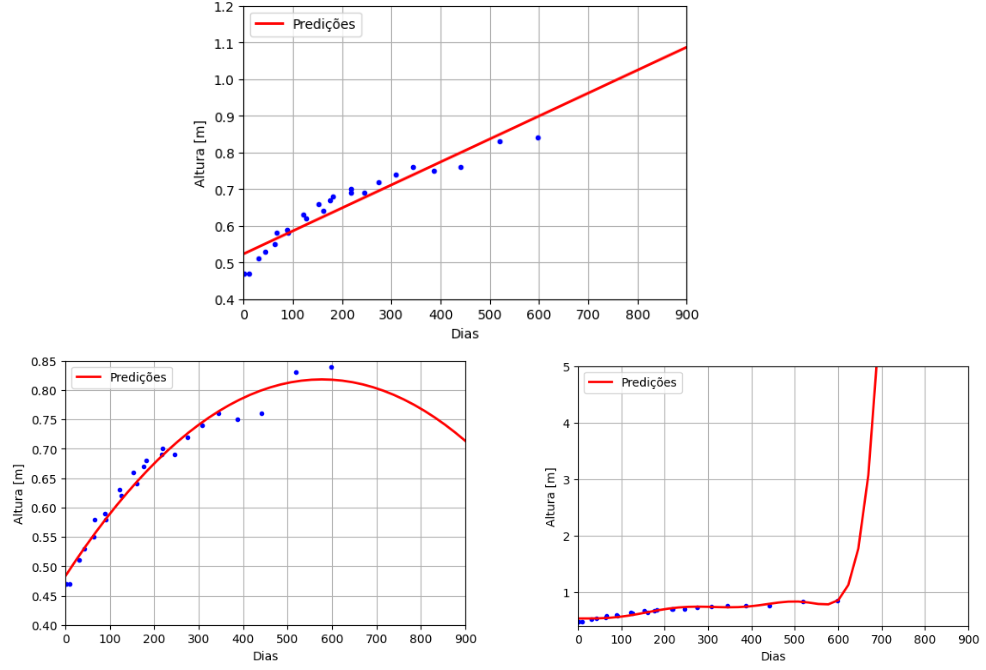
Figura 5: Extrapolação dos três modelos até 900 dias. Fonte: Próprio autor.
A reta obtida nunca desacelera e, se extrapolar ainda mais, o modelo linear prevê que antes dos 7 anos de idade a criança já teria 2 metros de altura. A parábola descreveu bem os dados até 600 dias, mas depois disso a altura começa a decair. Já o polinômio de grau 8 “explode” e em poucos dias pós o dia 600 já está em mais de 5 metros.
Antes de propor uma solução ao problema, deve-se alinhar as expectativas. É suficiente descrever o intervalo original dos dados? Nesse caso, os dados de altura de outros bebês poderiam ser ajustados e comparados com as Figuras 2-4 anteriores. Os próprios coeficientes dos polinômios poderiam servir de comparação para as diferentes taxas de crescimento, em vez de ter que plotar todos os gráficos no intervalo. Nesse contexto há o conceito de generalização, quando o modelo ajustado é capaz de obter informações ou realizar tarefas sobre dados novos, diferentes daqueles que foram utilizados para ajustar o modelo. A outra expectativa é se é necessário tentar prever o comportamento em um intervalo diferente, problema discutido anteriormente e conhecido como extrapolação [5]. Uma discussão sobre generalização e extrapolação, com exemplos em medicina, é encontrada em [6]. Claramente são problemas diferentes e utilizar a mesma técnica para ambos pode não ser suficiente.
Se não é possível mexer nos dados, o que resta é buscar modelos mais adequados. É claro que não precisam ser polinômios. Um dos apelos das redes neurais profundas segue nessa direção. Em [7], os autores discutem o trabalho de Cybenko [8], em que ele demonstrou o teorema da aproximação universal. O autor argumenta que uma rede neural com uma camada de saída linear e pelo menos uma camada oculta com função de ativação com certas propriedades é capaz de representar uma variedade muito grande de funções. Isso quer dizer que uma grande rede neural provavelmente vai ser capaz de representar a função. Só que a rede neural precisa ser treinada para isso e não há garantias que após o treinamento essa representação estará 100% correta.
Veja que o desafio muda. Como treinar a rede neural para que ela represente bem uma função e para que ela generalize bem para novos dados, sem overfitting? Será que ela vai precisar treinar com dados de alturas de quantos bebês para conseguir ter bons resultados? Será que precisa de modelos tão complexos para representar essa informação? Ou será que podemos seguir com a abordagem convencional de ver média e desvio padrão das alturas de uma população de bebês? Não existem respostas únicas e a beleza das ciências é essa, um espaço para discussão de ideias e desenvolvimento de novos modelos, teorias e tecnologias.
REFERÊNCIAS BIBLIOGRÁFICAS
[1] https://commons.wikimedia.org/wiki/File:Pyplot_overfitting.png
[2] https://creativecommons.org/licenses/by/4.0/deed.en
[3] DEISENROTH, M. P.; FAISAL, A. A.; ONG, C. S. Mathematics for Machine Learning. Cambridge, UK: Cambridge University, 2020. 371 p., il. ISBN: 9781108455145
[4] https://scikit-learn.org/1.5/modules/generated/sklearn.linear_model.LinearRegression.html
[5] https://online.stat.psu.edu/stat462/node/185/
[6] ALTMAN, D. G; BLAND, J M.. Statistics Notes: generalisation and extrapolation. BMJ, [S.L.], v. 317, n. 7155, p. 409-410, 8 ago. 1998. BMJ. http://dx.doi.org/10.1136/bmj.317.7155.409.
[7] GOODFELLOW, I.; BENGIO, Y.; COURVILLE, A. Deep learning. Cambridge, USA: MIT Press, 2017. 775 p., il. ISBN 9780262035613.
[8] CYBENKO, G.. Approximation by superpositions of a sigmoidal function. Mathematics Of Control, Signals, And Systems, [S.L.], v. 2, n. 4, p. 303-314, dez. 1989. Springer Science and Business Media LLC. http://dx.doi.org/10.1007/bf02551274.



