Uma não tão breve história do magnetismo (V.6. N.5. P.9, 2023)
Estimated reading time: 36 minute(s)
O fenômeno do magnetismo está bem longe de ser algo novo para nós, pois já na idade antiga era conhecido que algumas pedras achadas na região de Magnésia, Anatólia, na atual Turquia, possuíam a capacidade de atrair outras pedras ou inclusive pedaços de ferro. Estas pedras seriam posteriormente chamadas de Magnetita, cuja composição é apenas ferro e oxigênio em proporções 3:4, ou seja, óxido de ferro com fórmula Fe3O4. Pequenas agulhas deste material já eram usadas para navegação, pois estas agulhas ficam todas alinhadas sempre na mesma direção. Hoje sabemos que essa direção em que estas agulhas apontam é a direção do campo magnético da terra, que entre outras coisas, cria uma blindagem contra as partículas carregadas vindo do espaço e do sol que inviabilizariam a vida na terra. Este tipo de interação era diferente de outra conhecida, na qual dois objetos podiam se repelir ou atrair; hoje sabemos que essa é a força eletrostática.

O interesse em explicar a origem destes fenômenos de forma sistemática só veio depois do renascimento, e desde então houve grandes contribuições de pesquisadores da época para a sua compreensão. Nomes como Karl-Friedrich Gauss, Charles Coulomb, Hans Christian Ørsted, André-Marie Ampère, Michael Faraday, Nikola Tesla e James Clerk Maxwell fizeram grandes contribuições para entender os fenômenos eletromagnéticos, e todo esse trabalho pode ser resumido através das equações de Maxwell. São 4 equações, cada uma tem seu nome: lei de Gauss (efeitos das interações de distribuições de cargas em repouso, ou uma forma geral da lei de Coulomb), lei de Faraday (criação de uma tensão elétrica por variações em campos magnéticos e vice versa – princípio de funcionamento dos geradores de eletricidade e motores elétricos), lei de Gauss magnética (inexistência de cargas magnéticas) e lei de Ampère-Maxwell (interações de correntes elétricas com campos magnéticos e elétricos). Estas equações ajudam a entender as manifestações macroscópicas das interações entre cargas e correntes elétricas com campos elétricos e magnéticos; em particular para os campos magnéticos, consideramos o movimento de cargas livres, movimento de cargas em torno de posições de equilíbrio, e os movimentos internos dos elétrons na matéria. Contudo, não explicam a origem microscópica destas interações.

O caso do magnetismo é bastante curioso pois surge do movimento de cargas elétricas. Por isso não se fala em “cargas magnéticas”, porque a natureza deste fenômeno está relacionado diretamente com o fato da matéria possuir carga elétrica e ela estar em movimento no espaço. Se vocês aproximarem uma bússola de um fio de cobre pelo qual passa uma corrente constante, observarão a mudança na direção da bússola (veja vídeo acima). Da mesma forma em que temos a lei de Coulomb para descrever as forças entre cargas elétricas em repouso (cargas opostas se atraem e cargas iguais se repelem), a força que descreve a interação entre cargas em movimento é chamada de força magnética, e a combinação desta força com a lei de Coulomb leva à força de Lorentz. Esta força depende do tipo de carga, da direção e rapidez com que ela se desloca (a corrente elétrica), e da sua interação com outras cargas em movimento (campo magnético). A pergunta agora é como usar isto para explicar a resposta intrínseca da agulha da bússola, que não precisa de correntes para interagir com o campo magnético criado pela corrente. Para isto, precisamos de alguns conceitos de mecânica quântica, que foi desenvolvida no início do século XX.
Você se lembra do modelo do átomo? Isso mesmo! Pode ser o mais simples, aquele do núcleo e os elétrons girando em torno do núcleo em órbitas. O modelo atômico de Bohr. Esse modelo nos ajuda a visualizar o átomo ao considerar que esses elétrons que estão em movimento em torno do núcleo criam uma corrente, que por sua vez pode interagir com/criar um campo magnético. Esta propriedade, apesar de simplificada, é bem estudada e tem um nome: momento magnético (neste caso específico se chama de momento magnético orbital, pois é decorrente do elétron orbitar o núcleo). Além do momento magnético orbital, temos uma outra propriedade intrínseca do elétron, onde ele possui um momento magnético intrínseco, que chamamos de spin. De forma extremamente simplificada, é como se o elétron fosse uma esfera carregada que está girando em torno de si mesmo. Se juntarmos estes dois momentos magnéticos por cada elétron livre (veja figura e texto abaixo) teremos um momento magnético efetivo para cada átomo, dependendo das suas propriedades intrínsecas e das regras impostas pela mecânica quântica. De forma bem, mas beeeem simplificada, isto equivale a como se cada átomo estivesse gerando seu próprio campo magnético.
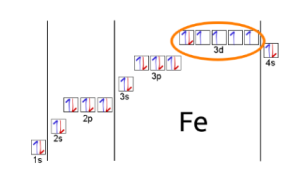
A configuração eletrônica de um átomo não é mais do que a forma em que os elétrons vão preenchendo os diferentes orbitais atômicos. Dependendo do orbital, eles vão formando pares que cancelam os momentos magnéticos criados por cada elétron de forma separada. Para o ferro, por exemplo, temos 26 elétrons: no primeiro orbital (a caixa mais à esquerda na figura) temos 2 elétrons apenas, no segundo orbital teremos 8 elétrons, no terceiro orbital serão 14 e no último teremos apenas 2. A chave está no terceiro orbital, porque por causa de regras específicas vindas da mecânica quântica teremos que 4 elétrons vão ficar sem par, e neste caso chamamos esses elétrons de não emparelhados. Como todos eles estão com o mesmo spin, contribuem para ter um momento magnético diferente de zero para o átomo de ferro. Isto para um átomo. Como será juntarmos 6.23×10²³ (~602.300.000.000.000.000.000.000 de) átomos? Cada um destes pequenos campos magnéticos de cada átomo irá contribuir para obtermos uma resposta macroscópica do material.
Neste modelo podemos ter cada momento magnético efetivo por cada átomo interagindo com um campo magnético externo, e o resultado será um alinhamento de todos estes momentos efetivos na direção do campo magnético externo. Isto é conhecido como paramagnetismo. Uma vez o campo é removido, os momentos magnéticos voltam a ficar em direções aleatórias, porque claro, não podemos esquecer que temos que levar em consideração que há energia térmica no material que implica que sua temperatura está acima do zero absoluto, e faz com que os momentos magnéticos apontem em direções aleatórias. Quanto maior a temperatura maior a aleatoriedade, e aleatoriedade implica soma zero, neste caso dos momentos magnéticos. Outro cenário possível é que exista um campo magnético intrínseco que faça com que cada momento magnético no material fique alinhado de forma espontânea; isto é conhecido como ferromagnetismo, e corresponde ao que observamos nos ímãs, por exemplo. Podemos transformar esse ímã em um material paramagnético, basta remover esse campo magnético intrínseco aumentando a temperatura do material, sendo que a temperatura na qual ocorre esta mudança é conhecida como temperatura de transição magnética.
Os ímãs se comportam da forma que conhecemos porque existe uma interação entre momentos magnéticos que faz com que eles sejam forçados a ficar paralelos entre eles. Esta interação está diretamente relacionada com o princípio de exclusão de Pauli, um efeito puramente quântico que diz que duas ‘partículas’ idênticas não podem estar descritas pelas mesmas propriedades quânticas, ou em outras palavras pelo mesmo estado. Como cada átomo possui elétrons que participam das ligações, a forma em que estes elétrons se acomodam para formar estas ligações vai determinar a forma em que os momentos magnéticos de cada átomo se organizam entre eles, evitando violar o princípio de exclusão de Pauli. Isto é conhecido como interação de troca e, para os ímãs, implica que os momentos magnéticos dos átomos se alinham de forma paralela. Se eles se acoplam de forma antiparalela teremos antiferromagnetismo, onde apesar de termos interações entre átomos, este material não irá se comportar como um ímã. A magnetita é ferrimagnética, pois o Fe possui dois tipos diferentes de momento magnético de acordo com seu estado de valência, e estes dois tipos de momento magnético se acoplam de forma antiparalela, mas macroscópicamente não há cancelamento da magnetização. Louis Néel ganhou o prémio Nobel em 1970 por descobrir isto.
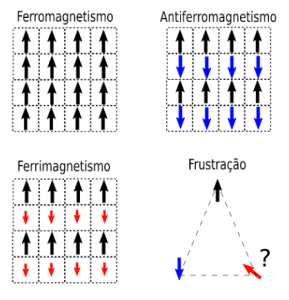
Agora imagine uma situação bastante curiosa: temos 3 átomos localizados nos vértices de um triângulo. Vamos supor que estes átomos possuem momentos magnéticos que se acoplam de forma antiparalela entre eles, e portanto deveria surgir ordenamento antiferromagnético. O primeiro átomo pode se acoplar efetivamente com o segundo e ficam antiparalelos, mas para este primeiro átomo ficar antiparalelo com o terceiro precisaremos que o segundo e o terceiro momento magnético se acople de forma paralela, violando nossa suposição inicial. Essas condições frustram o ordenamento magnético, e por isso é chamado de magnetismo frustrado. Usualmente os materiais com estas características conseguem atingir o estado ordenado, porém, a temperaturas muito mais baixas do que deveria ser esperado, e isto está associado com a dificuldade do sistema atingir uma situação de equilíbrio, ou com precisar reduzir a influência da temperatura o suficiente para que estas interações magnéticas possam atingir um estado de equilíbrio. Existem situações nas quais a temperatura para atingir este estado de equilíbrio é efetivamente zero, e como um material na temperatura do zero absoluto viola a terceira lei da termodinâmica, teremos que este material não se ordena efetivamente. Os spins neste caso se comportam como as moléculas de um líquido, onde temos interações entre os momentos (moléculas) mas sem desenvolver um estado ordenado. Estes materiais são chamados de líquidos de spin.
Podemos ter ainda outro cenário chamado de vidro de spin, no qual conseguimos induzir um estado em um material no qual há uma transição do estado paramagnético para um magnético no qual os momentos magnéticos estão em direções aleatórias, mas fixas. Este cenário é fácil de entender se compararmos com um material ferromagnético e observarmos o que é diferente neste caso: para o ferromagnetismo temos que o alinhamento dos momentos magnéticos é o mesmo para todos os momentos magnéticos, já no vidro de spin temos que este alinhamento é preservado porém com periodicidade na escala atômica bem reduzida. Isto também é conhecido como ordenamento magnético de curto alcance, e os materiais com estas características se chamam de vidros de spin porque o vidro possui o mesmo padrão, mas em relação ao ordenamento dos átomos e a formação de estruturas periódicas de átomos. E da mesma forma que o vidro, o vidro de spin pode estabilizar em um número extremamente grande de possíveis configurações de orientações de momentos magnéticos uma vez a temperatura do material se encontra abaixo o suficiente para induzir a transição.
Descrever teoricamente este tipo de situação era um grande desafio em meados do século XX, porque apesar que a teoria do magnetismo tinha sido amplamente desenvolvida nas bases da teoria quântica, era praticamente impossível formular uma teoria que pudesse descrever macroscópicamente a situação na qual tinha-se acoplamentos entre momentos magnéticos de forma aleatória. Um primeiro passo foi considerar a possibilidade de ter interações ferro e antiferromagnéticas entre momentos magnéticos diferentes no mesmo material, de forma que a média destas interações fosse equivalente a ter uma interação efetiva igual a zero (como um paramagnético) mas cujo desvio do zero fosse dependente da separação entre momentos magnéticos na rede cristalina. Para ser mais específicos, este desvio das interações seria cada vez menor se os momentos magnéticos aumentam sua distância.
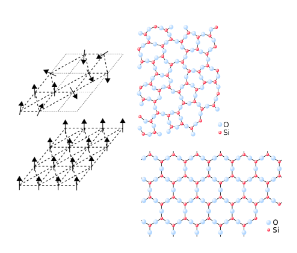
A ideia por trás do ordenamento do vidro de spin é valorizar o ordenamento em função do tempo e não do espaço, lembrando que os fenômenos na escala microscópica não necessariamente acontecem da mesma forma que as respostas macroscópicas. Como entender isto? De forma bem simplificada, isto equivale a que quando o ordenamento acontecer, não vai importar mais em qual direção o momento magnético aponta, e o que vai ser relevante é que ele “lembre” desta mudança de orientação. Ao considerar todos os momentos magnéticos, podemos fazer uma média macroscópica de todas as interações para poder comparar com o observado no laboratório. Para encaixar isso em modelos matemáticos, foi criado o truque da réplica, que consiste em supor que esta média macroscópica não é mais do que muitas cópias de pequenos segmentos do meu material que eu consigo modelar de uma forma conhecida. Porém, isto não era suficiente para justificar que em um vidro de spin poderíamos ter differentes possíveis configurações dos momentos magnéticos, e o que foi proposto por Giorgio Parisi foi uma função matemática que permitiria quantificar que tão diferente é uma configuração de outra. Com isto, ficará claro que cada réplica vai lembrar da sua mudança de orientação.
A ideia apresentada no parágrafo acima pode parecer meio abstrata, mas podemos mencionar casos nos quais a teoria descrita acima serviu para descrever outras situações: o funcionamento de redes neuronais, tarefas de otimização de processos, processos de movimento de esferas emperradas, granularidade, o movimento de bandos de pássaros, e turbulência de fluidos (como as correntes de ar).
O magnetismo, ao ser um fenômeno quântico, também pode aparecer junto com outros fenômenos. Um exemplo é o do magnetismo e interações com carga elétrica (ferroeletricidade), com cargas elétricas livres (magnetoresisência), com redes cristalinas (magnetostricção e piezomagnetismo), a manipulação da temperatura de um material magnético através de campos magnéticos (efeito magnetocalórico), e a coexistência do magnetismo e a supercondutividade, que será tema de um próximo artigo.